你有没有想过,在工程设计和流体力学领域,如何精准计算管道流量?这不仅仅是一个技术问题,更是一个关乎效率与安全的重要课题。想象如果你正在设计一个供水系统,或者是一个工业管道网络,流量的大小直接关系到整个系统的性能。那么,当面对已知的压力和管径时,如何运用公式准确求出流量呢?这背后其实蕴含着丰富的物理原理和工程实践。
流量计算的基本原理
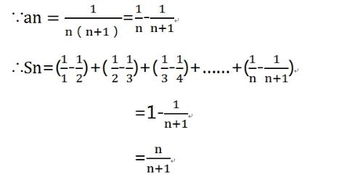
在深入探讨具体的计算方法之前,我们需要先理解流量计算的基本原理。流量,简单来说,就是单位时间内通过某一截面的流体量。在管道系统中,流量通常用符号Q表示,单位是立方米每秒(m3/s)或升每秒(L/s)。影响流量的因素有很多,包括管道的直径、压力差、流体的性质(如密度和粘度)以及管道的粗糙度等。
以圆管道为例,流量的计算公式可以简化为:流量Q = (πD2/4) × V,其中D是管道直径,V是流速。这个公式看似简单,但在实际应用中,流速V的确定往往需要考虑更多因素。比如,流体的粘性会导致摩擦阻力,管道内壁的粗糙度也会影响流速。这些因素使得流量计算变得复杂,需要借助更精确的公式和模型。
伯努利方程与流量计算

在已知压力和管径的情况下,伯努利方程是一个非常有用的工具。伯努利方程描述了在流体中沿一条流线的运动过程中的能量守恒。它表达了流体在流动过程中,压力能、动能和势能之间的转换关系。具体来说,伯努利方程可以表示为:
P? + (1/2)ρV?2 + ρgh? = P? + (1/2)ρV?2 + ρgh?
其中,P?和P?表示管道内部的压力,ρ表示流体的密度,V?和V?表示流体在管道两端的速度,g表示重力加速度,h?和h?表示流动过程中的高度差。
假设你有一个水平放置的管道,即h? = h?,那么伯努利方程可以简化为:
P? + (1/2)ρV?2 = P? + (1/2)ρV?2
如果管道两端存在压力差(P? ≠ P?),那么可以通过这个方程计算出流速V。一旦知道了流速,再结合管道的截面积,就可以计算出流量Q。
实际应用中的修正与调整
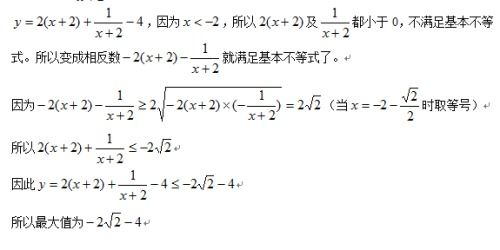
在实际工程中,仅仅依靠伯努利方程往往不够。管道内的阻力损失,如摩擦阻力、局部阻力等,都需要考虑进去。这些阻力会导致流体的能量损失,从而影响实际流量。为了更准确地计算流量,工程师们通常会引入一些修正系数,如摩擦系数和局部阻力系数。
以圆管道为例,流速的计算公式可以写为:
V = (2g(P? - P?) / (ρL))^(1/2) / (1 + fL/D)
其中,L是管道长度,f是摩擦系数,D是管道直径。摩擦系数f与流体的雷诺数Re和管道的相对粗糙度(管道内壁粗糙度与管径之比)有关。雷诺数Re是一个无量纲数,用来描述流体的流动状态。当雷诺数较低时,流体流动较为平稳,称为层流;当雷诺数较高时,流体流动较为紊乱,称为湍流。
在实际应用中,雷诺数Re可以通过以下公式计算:
Re = (ρVD) / μ
其中,μ是流体的动态粘度。通过计算雷诺数Re,可以查表或使用经验公式确定摩擦系数f。
流量计算公式的具体应用
现在,让我们通过一个具体的例子来演示如何利用上述公式计算流量。假设你有一个直径为0.1米的水平圆管道,管道入口处的压力为500帕斯卡,出口处的压力为400帕斯卡,流体的密度为1000千克每立方米,动态粘度为0.001帕斯卡秒,管道长度为10米,管道内壁的相对粗糙度为0.0015。
首先,计算雷诺数Re:
Re = (1000 × 0.1 × 1) / 0.001 = 100,000
根据雷诺数Re和相对粗糙度,查表或使用经验公式确定摩擦系数f。假设f = 0.02。
接下来,计算流速V:
V = (2 × 9.8 × (500 - 400) / 1000)^(1/2) / (1 + 0.02 × 10 / 0.1) ≈ 0.283 米每秒
计算流量Q:
Q = (π × 0.

